单位圆

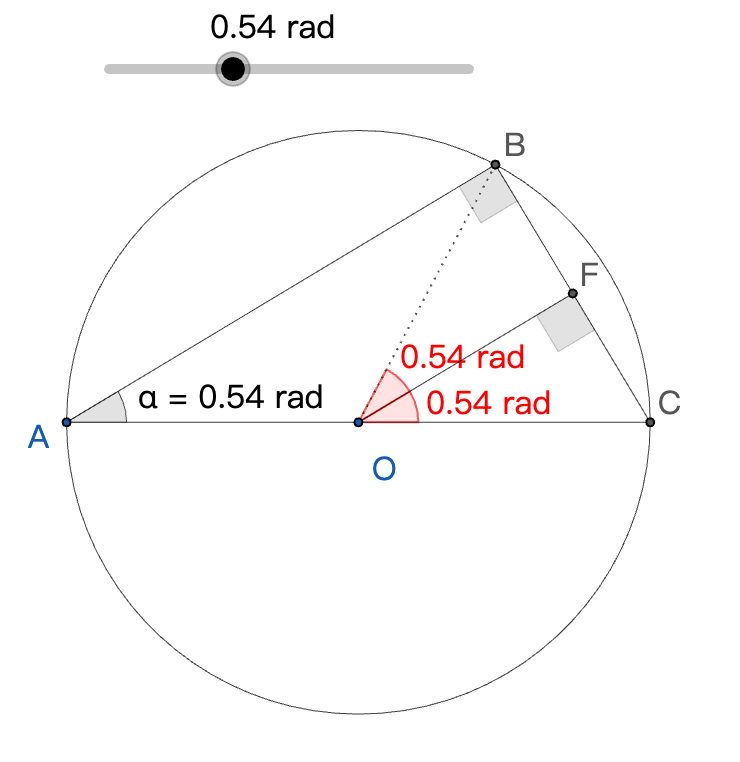
单位圆是半径为1的圆，圆心在坐标原点。基于弧度的概念，在单位圆中，圆心角的弧度恰好等于其对应弧长。通过它可以将三角函数的定义从直角三角形扩展到任意角度。

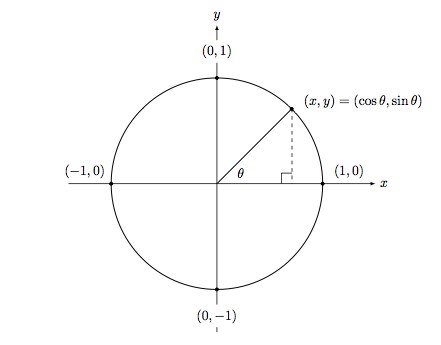
单位圆的定义 单位圆的基本特征：

• 圆心在坐标原点(0,0)
• 半径为1个单位
• 任意点P(x,y)满足方程$x^2+y^2=1$
• 逆时针方向为正角度

与三角函数的关系

• $x=\cos \theta$
• $y=\sin \theta$
• $\tan \theta =\frac{y}{x}=\frac{\sin \theta }{\cos \theta }$ 其中$\theta$是从正x轴到点P的角度

角度与弧度

• $2\pi$ 弧度 = $360°$
• $\pi$ 弧度 = $180°$
• 弧度 = $\frac{\pi }{180}$ × 角度
• 角度 = $\frac{180}{\pi }$ × 弧度

特殊角度值

|角度|弧度|sin|cos| |---|---|---|---| |0°|0|0|1| |30°|$\frac{\pi }{6}$|$\frac{1}{2}$|$\frac{\sqrt{3}}{2}$| |45°|$\frac{\pi }{4}$|$\frac{\sqrt{2}}{2}$|$\frac{\sqrt{2}}{2}$| |60°|$\frac{\pi }{3}$|$\frac{\sqrt{3}}{2}$|$\frac{1}{2}$| |90°|$\frac{\pi }{2}$|1|0|

重要性质

1. 对称性：

• sin在y轴对称

• cos在x轴对称

2. 周期性：

• sin和cos的周期是$2\pi$
• 每转一圈回到相同位置

弧长公式 $\theta$，其中 $\theta$ 是弧度制的角度。

单位圆上的弧长 =

面积关系 $\frac{\theta }{2}$，其中 $\theta$ 是弧度制的角度。

单位圆的扇形面积 =

应用场景

1. 扩展三角函数定义域
2. 研究周期性运动
3. 复数的几何表示
4. 三角恒等式证明
5. 波动现象分析