三角恒等式

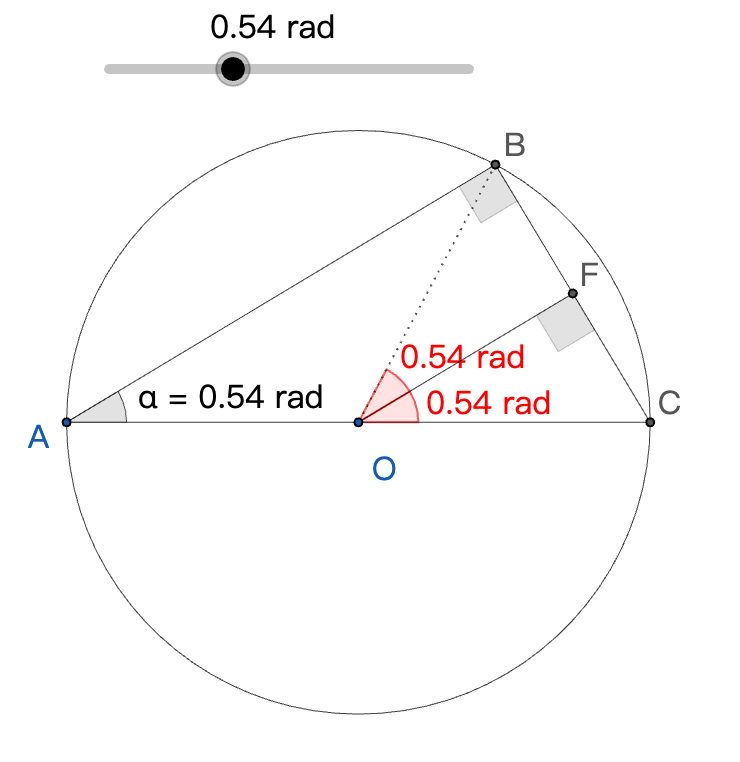
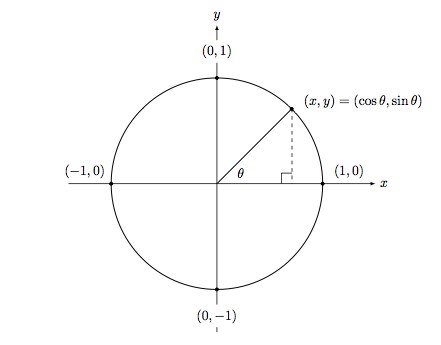
三角恒等式起源于单位圆的推导。

1. 倍角公式： sin 2θ = 2 sin θ cos θ cos 2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ

2. 半角公式： sin²(θ/2) = (1 - cos θ) / 2 cos²(θ/2) = (1 + cos θ) / 2

3. 和差公式： sin(A ± B) = sin A cos B ± cos A sin B cos(A ± B) = cos A cos B ∓ sin A sin B

4. 和差化积： sin A + sin B = 2 sin((A+B)/2) cos((A-B)/2) cos A + cos B = 2 cos((A+B)/2) cos((A-B)/2)

• 公式：
  • 和差公式： $\sin (\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$ $\cos (\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$
  • 倍角公式： ${\sin }^2\theta +{\cos }^2\theta =1$

勾股恒等式 三角同余恒等式 和差化积 二倍角公式 积化和差