弧度

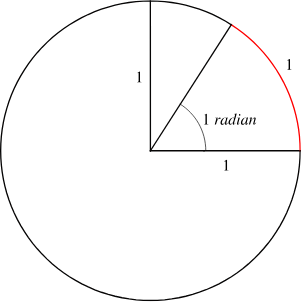
弧度的定义

弧度是一种角的度量单位，用弧长与半径的比值表示的角度，称为弧度。

1弧度：从单位圆的圆心出发，圆上取弧长为 1的两点 ，则和圆心构成的夹角为一个弧度的角。 一个完整的圆是 2π 弧度，所以每 2π 弧度有 360 度，等于 180 度/π 或 57.29577951 度/弧度。直角是 π/2 弧度。

一个直角的弧度测量值是多少？

因为直角在度上是 90°，所以我们有： 90° = 90° × $\frac{\pi }{180°}$ = $\frac{\pi }{2}$ 弧度。

角度弧度转换

角度与弧度之间的转换：

角度 𝜃 以弧度为单位的测量值就是该角度所切出的圆的弧长。从一些简单的例子开始。如果角度以度来测量是 0°，那么该角度所切出的圆的弧长是 0。另一方面，如果角度以度来测量是 360°，那么该角度所切出的圆的弧长是半径为 1 的圆的周长，即 2𝜋⋅1=2𝜋。

1. 要将以度为单位的测量值转换为弧度，乘以$\frac{\pi }{180°}$。
2. 要将以弧度为单位的测量值转换为度，乘以$\frac{180°}{\pi }$。

弧长公式

弧长公式

对于半径为$r$的一般圆，如果与正$x$轴形成一个角度$\theta$（以弧度给出），那么该角度切出的圆的部分弧长为： (弧长) = r $\theta$。 正如我们所看到的，对于半径$r=1$的圆，弧长就是弧度制下的角度$\theta$。

例题

将下列角度从度转换为弧度： $60^{\circ }$，$180^{\circ }$。

因为$2\pi$弧度$=360^{\circ }$，所以我们有： $60^{\circ }=60^{\circ }\cdot \frac{2\pi }{360^{\circ }}=\frac{\pi }{3}$弧度， $180^{\circ }=180^{\circ }\cdot \frac{2\pi }{360^{\circ }}=\pi$弧度。

扇形面积

例题

Example

在上图中，哪个阴影部分更大？ (小圆圈的大小都一样。)

通过弧度的几何直觉，可以建立起对弧度的直觉认知，理解它的几何意义，从而更好地掌握这个概念在三角函数和更高等数学中的应用。