集合运算

有几种有用的运算可以用来组合、比较和分析集合。

• 并集： 两个集合的并集，用$\cup$表示，是指至少在两个集合之一中的所有元素组成的集合。例如，$\{1,2,3\}\cup \{3,4,5\}=\{1,2,3,4,5\}$。在布尔逻辑中，并集表示为逻辑“或”。
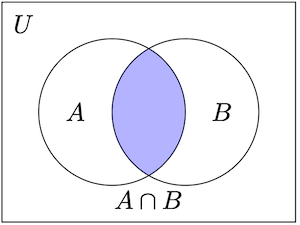
• 交集： 两个集合的交集，用$\cap$表示，是指同时在两个集合中的元素组成的集合。例如，$\{1,2,3\}\cap \{3,4,5\}=\{3\}$。在布尔逻辑中，交集表示为逻辑“与”。
• 补集（绝对）： 用${}^c$表示，绝对补集是指不在一个集合中的所有元素组成的集合。如果我们将全集$U$视为所有整数的集合，那么$\{1,2,3{\}}^c$将表示除1、2和3之外的所有整数。在布尔逻辑中，补集表示为逻辑“非”。
• 补集（相对）： 相对补集，用$\backslash$表示，是指在第一个集合中但不在第二个集合中的元素组成的集合。例如，$\{1,2,3\}\backslash \{3,4,5\}=\{1,2\}$。相对补集也可以用减号表示，即$\{1,2,3\}-\{3,4,5\}=\{1,2\}$。
• 对称差集： 对称差集，用$△$表示，是指在两个集合之一中但不在两个集合中的元素组成的集合。例如，$\{1,2,3\}△\{3,4,5\}=\{1,2,4,5\}$。在布尔逻辑中，对称差集表示为逻辑“异或”。

集合运算示例

1. $\{2,4,6\}\cup \{3,5,7\}$等于什么？

$\cup$符号表示两个集合的并集。

因此，$\{2,4,6\}\cup \{3,5,7\}=\{2,3,4,5,6,7\}$。$\square$

2. $\{5,3,2,6\}\cap \{7,1,6,2,8\}$的结果是什么？

$\cap$符号表示交集，即求两个集合中共同的元素。

所以$\{5,3,2,6\}\cap \{7,1,6,2,8\}=\{2,6\}$。

3. $\{7,5,9\}\cup \{0,1,5\}$的结果是什么？

并集是将两个集合中的所有元素合并在一起，去除重复元素。

所以$\{7,5,9\}\cup \{0,1,5\}=\{0,1,5,7,9\}$。

4. 已知$A=\{2,a^2-4a+7\}$，$B=\{a+1,a^2+1,a^2-1\}$，如果$A\cap B=\{4\}$，那么$a$是多少？

因为$A\cap B=\{4\}$，所以集合$A$和$B$都必须有$4$这个元素。

对于集合$A$，有$a^2-4a+7=4$，即$(a-1)(a-3)=0$，解得$a=1$或$a=3$。

当$a=1$时，集合$B=\{1+1,1^2+1,1^2-1\}=\{2,2,0\}$，此时$A\cap B=\{2\}\ne \{4\}$。

当$a=3$时，集合$B=\{3+1,3^2+1,3^2-1\}=\{4,10,8\}$，此时$A\cap B=\{4\}$。

所以满足$A\cap B=\{4\}$的$a$的值是$3$。$\square$

5. $\{2,4,6,8,10,12\}△\{3,6,9,12,15\}$等于什么？

$△$表示对称差集，即求在两个集合之一中但不在两个集合中的元素。

所以$\{2,4,6,8,10,12\}△\{3,6,9,12,15\}=\{2,3,4,8,9,10,15\}$。$\square$

集合基础