集合论

集合是一组无序的元素的集体，是理解组合数学、概率论和数论的基础数据结构。集合的思想方法和分类思维、逻辑思维、决策思维、系统思维有密切关系，维恩图是分析集合元素关系问题的重要方法。

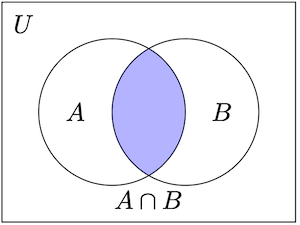
U

集合的全集

补集

集合的基本概念

1. 定义：用花括号表示的无序元素组
2. 特点：
   • 元素无序：$\{1,2,3\}=\{2,3,1\}$
   • 元素唯一：$\{1,1,1\}=\{1\}$
3. 表示方法：$A=\{a,b,c\}$

集合运算 $\cup$ | 至少在一个集合中 | $\{1,2\}\cup \{2,3\}=\{1,2,3\}$ | | 交集 | $\cap$ | 同时在两个集合中 | $\{1,2\}\cap \{2,3\}=\{2\}$ | | 补集 | ${}^c$ | 不在该集合中的元素 | $\{1,2{\}}^c=U-\{1,2\}$ | | 相对补 | $\backslash$ | 在A不在B中的元素 | $\{1,2\}\backslash \{2\}=\{1\}$ | | 对称差 | $△$ | 只在其中一个集合中 | $\{1,2\}△\{2,3\}=\{1,3\}$ |

| 运算 | 符号 | 含义 | 示例 | |------|------|------|------| | 并集 |

重要定理

1. 德摩根律：
   • $(A\cup B{)}^c=A^c\cap B^c$
   • $(A\cap B{)}^c=A^c\cup B^c$
2. 容斥原理：
   • $|A\cup B|=|A|+|B|-|A\cap B|$

例题1：集合等价性

• $A=\{1,3,5,7,9\}$
• $B=\{1,2,3,4,5,6\}$
• $D=\{5,4,2,6,1,3\}$

解答：$B$和$D$等价，因为包含相同元素

例题2：代数集合

• $A=\{2,a^2-4a+7\}$

• $B=\{a+1,a^2+1,a^2-1\}$ 若$A\cap B=\{4\}$，求$a$的值

解答：

1. $a^2-4a+7=4$
2. $(a-1)(a-3)=0$
3. $a=3$（验证$a=1$不符合）

例题3：德摩根律应用

• $U=\{1,2,3,4,5,6,7,8,9\}$

• $A=\{2,5,7,3,1\}$

• $B=\{9,8,7,5,2\}$ 求$A^c\cup B^c$

解答：使用德摩根律

1. $A\cap B=\{2,5,7\}$
2. $(A\cap B{)}^c=\{1,3,4,6,8,9\}$
3. 由德摩根律，$A^c\cup B^c=(A\cap B{)}^c$

集合基础 集合运算 集合关系 基数