集合运算是对集合进行的基本数学操作,包括并、交、差、补等运算,是解决实际问题的重要数学工具。
- 并集:A∪B={x∣x∈A 或 x∈B}
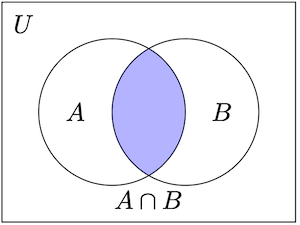
- 交集:A∩B={x∣x∈A 且 x∈B}
- 差集:A−B={x∣x∈A 且 x∈/B}
- 补集:A′={x∣x∈U 且 x∈/A}(U为全集)
- 对称差集:用△表示,是指在两个集合之一中但不在两个集合中的元素组成的集合。例如,{1,2,3}△{3,4,5}={1,2,4,5}。在布尔逻辑中,对称差集表示为逻辑“异或”。
重要运算律:
- 交换律:A∪B=B∪A
- 结合律:(A∪B)∪C=A∪(B∪C)
- 分配律:A∩(B∪C)=(A∩B)∪(A∩C)
- 德摩根律:(A∪B)′=A′∩B′
集合运算示例
- {2,4,6}∪{3,5,7}等于什么?
∪符号表示两个集合的并集。
因此,{2,4,6}∪{3,5,7}={2,3,4,5,6,7}。□
- {5,3,2,6}∩{7,1,6,2,8}的结果是什么?
∩符号表示交集,即求两个集合中共同的元素。
所以{5,3,2,6}∩{7,1,6,2,8}={2,6}。
- {7,5,9}∪{0,1,5}的结果是什么?
并集是将两个集合中的所有元素合并在一起,去除重复元素。
所以{7,5,9}∪{0,1,5}={0,1,5,7,9}。
- 已知A={2,a2−4a+7},B={a+1,a2+1,a2−1},如果A∩B={4},那么a是多少?
因为A∩B={4},所以集合A和B都必须有4这个元素。
对于集合A,有a2−4a+7=4,即(a−1)(a−3)=0,解得a=1或a=3。
当a=1时,集合B={1+1,12+1,12−1}={2,2,0},此时A∩B={2}={4}。
当a=3时,集合B={3+1,32+1,32−1}={4,10,8},此时A∩B={4}。
所以满足A∩B={4}的a的值是3。□
- {2,4,6,8,10,12}△{3,6,9,12,15}等于什么?
△表示对称差集,即求在两个集合之一中但不在两个集合中的元素。
所以{2,4,6,8,10,12}△{3,6,9,12,15}={2,3,4,8,9,10,15}。□
集合基础