Summary
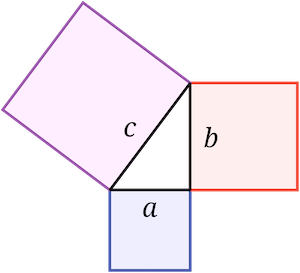
为什么说逢三角形而不决-->勾股定理?
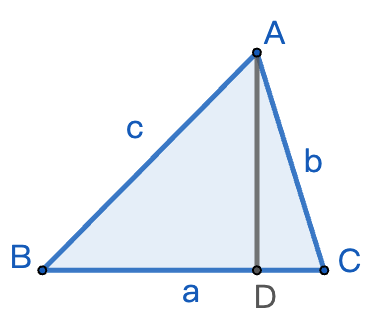
因为任意三角形都可分解成两个直角三角形啊!
-
给定三边长,求角度:
- 已知三角形 ABC 的三边长 a=3, b=4, c=5,求角 A 的大小。
讨论:
-
勾股定理只能直接应用于直角三角形。
-
这里我们需要利用余弦定理:
-
给定三边长,求面积:
- 问题:已知三角形 ABC 中,a=5, b=7, 角 A=40°,求边 c。
讨论:
- 这需要使用余弦定理的变形。
-
给定两条边及夹角,求面积:
- 已知三角形 ABC 中,a=6, b=8, 角 C=60°,求三角形的面积。
讨论:
-
勾股定理不适用,因为这不是直角三角形。
-
我们可以使用正弦公式求面积:
-
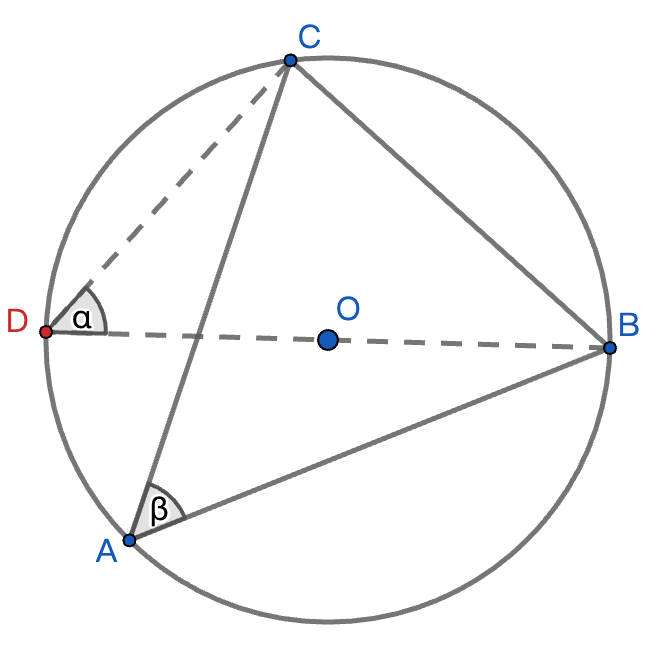
求三角形的外接圆半径:
- 问题:已知三角形 ABC 的三边长 a=3, b=4, c=5,求其外接圆半径。
讨论: 问题问答平台
给定两边和一个非夹角,求第三边:
- 问题:已知三角形 ABC 中,a=5, b=7, 角 A=40°,求边 c。
讨论:
- 这需要使用余弦定理的变形。
-
正弦定理:
-
余弦定理: (类似地, 和 的表达式)
graph TD
A[直角三角形] --> B[勾股定理: a² + b² = c²]
A --> C[一般三角形]
B -->|推广| C
C --> D[面积公式: S = ½ab·sinC]
C --> E[正弦定理: a/sinA = b/sinB = c/sinC]
E -->|等于| F[外接圆直径: 2R]
style A fill:#f9f,stroke:#333,stroke-width:2px
style C fill:#bbf,stroke:#333,stroke-width:2px
style E fill:#bfb,stroke:#333,stroke-width:2px