单位圆

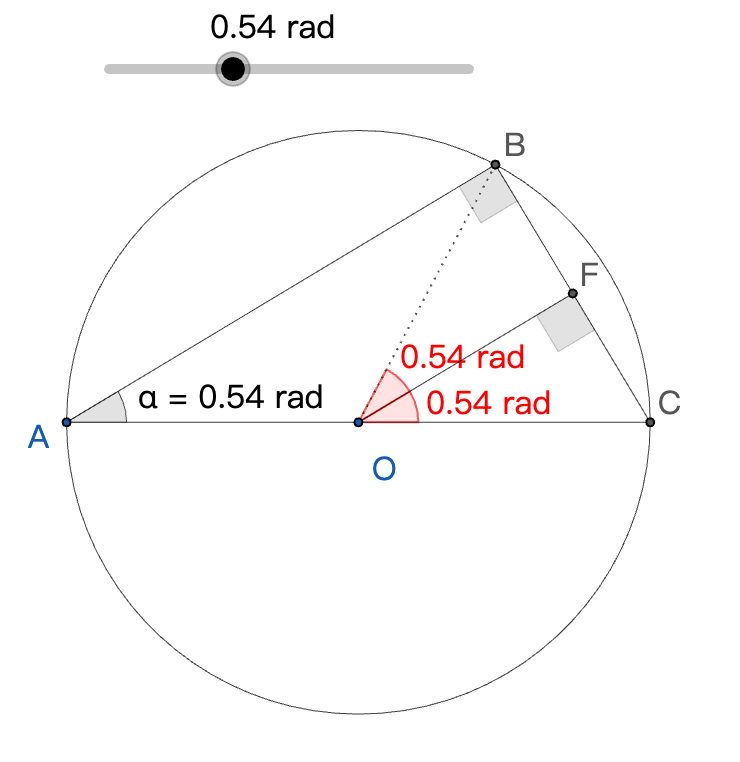
单位圆是半径为1的圆，圆心在坐标原点。基于弧度的概念，在单位圆中，圆心角的弧度恰好等于其对应弧长。

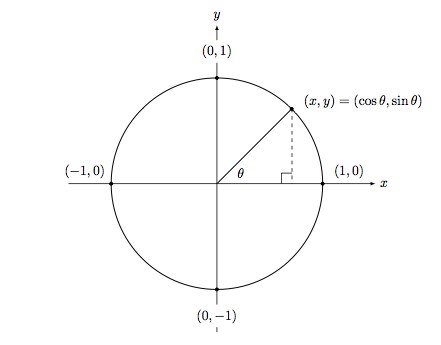
单位圆在三角函数中扮演着核心角色，单位圆上有哪些有趣的发现？

以下是一些主要的等量关系：

基本恒等式

${\sin }^2\theta +{\cos }^2\theta =1$ 这是单位圆上最基本的等量关系。

正切和余切关系：

$\tan \theta =\frac{\sin \theta }{\cos \theta }$ $\cot \theta =\frac{\cos \theta }{\sin \theta }$

正割和余割关系：

$\sec \theta =\frac{1}{\cos \theta }$ $\csc \theta =\frac{1}{\sin \theta }$

平方关系：

$1+{\tan }^2\theta ={\sec }^2\theta$ $1+{\cot }^2\theta ={\csc }^2\theta$

弧长公式

单位圆上的弧长 = $\theta$，其中 $\theta$ 是弧度制的角度。

面积关系

单位圆的扇形面积 = $\frac{\theta }{2}$，其中 $\theta$ 是弧度制的角度。

1. 性质：

   • 圆上任意点P(x,y)对应的角θ满足： x = cosθ, y = sinθ
   • tanθ = sinθ / cosθ

2. 特殊角：

   • 0°: (1, 0)
   • 30°: (√3/2, 1/2)
   • 45°: (√2/2, √2/2)
   • 60°: (1/2, √3/2)
   • 90°: (0, 1)

3. 象限： I: (+,+) II: (-,+) III: (-,-) IV: (+,-)