向量的线性组合是用标量乘以向量再求和的运算,是研究向量空间结构的基础工具。
基本定义
线性组合
对于向量组,其线性组合为: 其中为实数系数

线性相关性
判定方法
向量组线性相关 存在不全为零的系数使得:

张成空间
Span概念
向量组的所有线性组合构成的集合:

重要性质
-
线性组合的性质:
-
线性相关的性质:
- n个向量线性相关 n+1个向量线性相关
- 包含零向量的向量组必线性相关
几何解释
直观理解
- 二维情况:
一个向量:直线
两个线性无关向量:平面
- 三维情况:
- 两个向量:平面
- 三个线性无关向量:空间
常见错误
注意事项
- 混淆线性相关与平行
- 忽视零向量的特殊性
- 张成空间维数判断错误
练习方向
重点掌握
- 线性相关性判定
- 张成空间确定
- 基的选取
- 维数计算
扩展理解
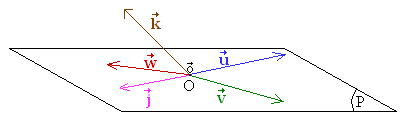
- 和是线性无关的,定义了二维平面 P;
- 、、是线性相关的;
- 和是线性相关的;
- 、、是线性无关的,三个向量定义了三维空间;
- 和是相关的,因为