向量的坐标表示和点表示

向量的坐标表示可以看成是从原点出发到坐标点的标准向量，或者看成$X$，$Y$方向上的位移。

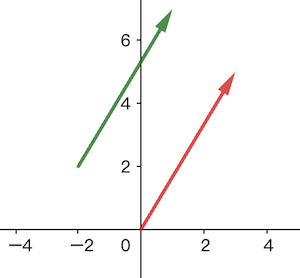
两种表示方法

1. 点表示：
   • 起点A$(x_1,y_1)$
   • 终点B$(x_2,y_2)$
   • 记作$\overrightarrow{AB}$
2. 坐标表示：
   • 向量$\vec{v}=(a,b)$
   • 其中$a=x_2-x_1$
   • $b=y_2-y_1$

转换关系

1. 点表示→坐标表示： $\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$

2. 坐标表示→点表示：

   • 任选起点$(x_1,y_1)$
   • 终点为$(x_1+a,y_1+b)$
   • 表示同一个向量

坐标表示的原点视角

1. 向量$(a,b)$可以理解为：
   • 从原点$(0,0)$出发
   • 到达点$(a,b)$的位移
   • 即$\overrightarrow{OP}$，其中O是原点
2. 向量的”标准位置”：
   • 起点在原点
   • 终点即坐标值
   • 所有向量都可以移到这个位置
3. 几何意义：
   • 向量是从原点出发的”箭头”
   • 坐标就是终点位置
   • 体现了位置和位移的统一
4. 优点：
   • 统一了点和向量的表示
   • 简化了理解难度
   • 建立了直观联系

本质联系

1. 位移观点：
   • 点表示强调起点到终点的移动
   • 坐标表示强调移动的量
2. 等价性：
   • 同一向量可有无数点表示
   • 但只有一个坐标表示
   • 体现了向量的平移不变性

应用场景

1. 点表示适合：
   • 几何问题
   • 路径描述
   • 位置变化
2. 坐标表示适合：
   • 向量运算
   • 代数处理
   • 计算机编程

常见误区

1. 混淆点和向量：
   • 点是位置
   • 向量是位移
2. 忽视起点作用：
   • 点表示需要起点
   • 坐标表示不依赖起点