定义
德摩根定律是一组在集合论和布尔代数中使用的重要规则,这些定律描述了逻辑运算”与”(AND)和”或”(OR)与”非”(NOT)运算之间的关系。
公式表示
对于任意两个命题 P 和 Q:
- 其中:
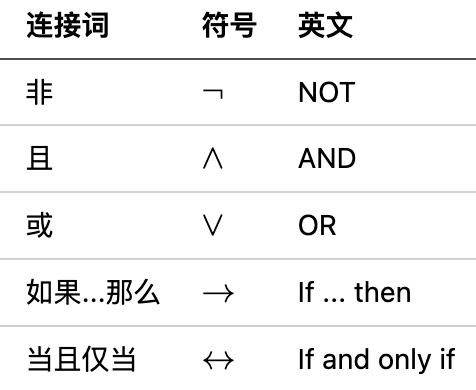
- 表示”非”(NOT)
- 表示”与”(AND)
- 表示”或”(OR)
- 表示”等价于”
口语表述
- “非(P 且 Q)“等价于”(非 P)或(非 Q)”
- “非(P 或 Q)“等价于”(非 P)且(非 Q)“
应用示例
- 集合论:
- A 和 B 的补集 = A 的补集 并 B 的补集
- A 或 B 的补集 = A 的补集 交 B 的补集
- 电路设计: 用于简化逻辑电路,减少所需的门电路数量。
- 程序设计: 优化条件语句,提高代码效率和可读性。
验证方法
可以通过真值表或代数方法验证德摩根定律的正确性。
重要性
德摩根定律在逻辑学、数学、计算机科学和电子工程等领域有广泛应用,是简化逻辑表达式和设计高效算法的重要工具。
相关概念
练习题
- 使用德摩根定律简化表达式:
- 在集合论中,证明: (A ∪ B)’ = A’ ∩ B’