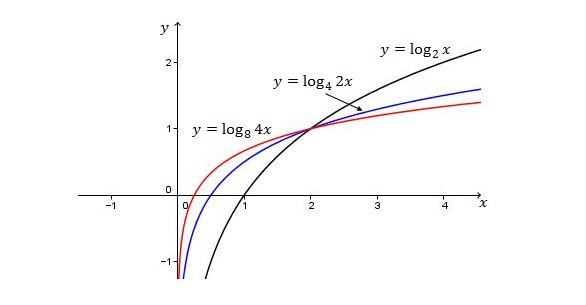对数函数的图像

一、对数函数图像的例题

题目
- 如果以下三条曲线相交于一点， $a$ 的值是多少？ $y = lo g_{2} x y = lo g_{4} 2 x y = lo g_{8} a x$
答案
- $a = 4$ 。
解析
- 首先我们找到 $y = lo g_{2} x$ 和 $y = lo g_{4} 2 x$ 相交的点。将第二个方程的底数转换：

lo g_{4} 2 x = lo g_{2^{2}} 2 x = \frac{1}{2} lo g_{2} 2 x = lo g_{2} (2 x)^{\frac{1}{2}} = lo g_{2} 2 x

然后令 $lo g_{2} x = lo g_{2} 2 x$ ，得到 $x = 2 x \Rightarrow x^{2} = 2 x$ ，这意味着 $x (x - 2) = 0 \Rightarrow x = 2$ （因为对数函数定义在正数上）。当 $x = 2$ 时， $y = lo g_{2} x$ 的值为 $lo g_{2} 2 = 1$ ，这意味着前两条曲线相交于点 $(2, 1)$ 。
现在，对于第三条曲线 $lo g_{8} a x$ 要通过 $(2, 1)$ ，必须有 $lo g_{8} (a \cdot 2) = 1$ ，这意味着 $2 a = 8$ 。因此，答案是 $a = 4$ 。三条函数的图像如下图所示。 $_{□}$

题目
- 曲线 $lo g_{\frac{1}{3}} x$ 在 $x > a$ 时位于曲线 $lo g_{\frac{1}{5}} x$ 下方， $a$ 的值是多少？
答案
- $a = 1$ 。
解析
- 因为无论底数如何， $1$ 的对数总是 $0$ ，所以 $lo g_{\frac{1}{3}} 1 = lo g_{\frac{1}{5}} 1 = 0$ ，所以我们知道两条曲线在点 $(1, 0)$ 相交。对于任何 $x > 1$ ，我们知道 $lo g_{3} x > lo g_{5} x \Rightarrow lo g_{\frac{1}{3}} x < lo g_{\frac{1}{5}} x$ 。对于任何 $x < 1$ ，我们知道 $lo g_{3} x < lo g_{5} x \Rightarrow lo g_{\frac{1}{3}} x > lo g_{\frac{1}{5}} x$ 。因此，两条曲线的图像如下图所示：
- 因为 $lo g_{\frac{1}{3}} x$ 在 $x > 1$ 时位于 $lo g_{\frac{1}{5}} x$ 下方，所以答案是 $a = 1$ 。 $_{□}$