函数的单调性描述了函数值随自变量变化的增减趋势,是分析函数行为的重要工具。
函数单调性学习卡片
基本定义
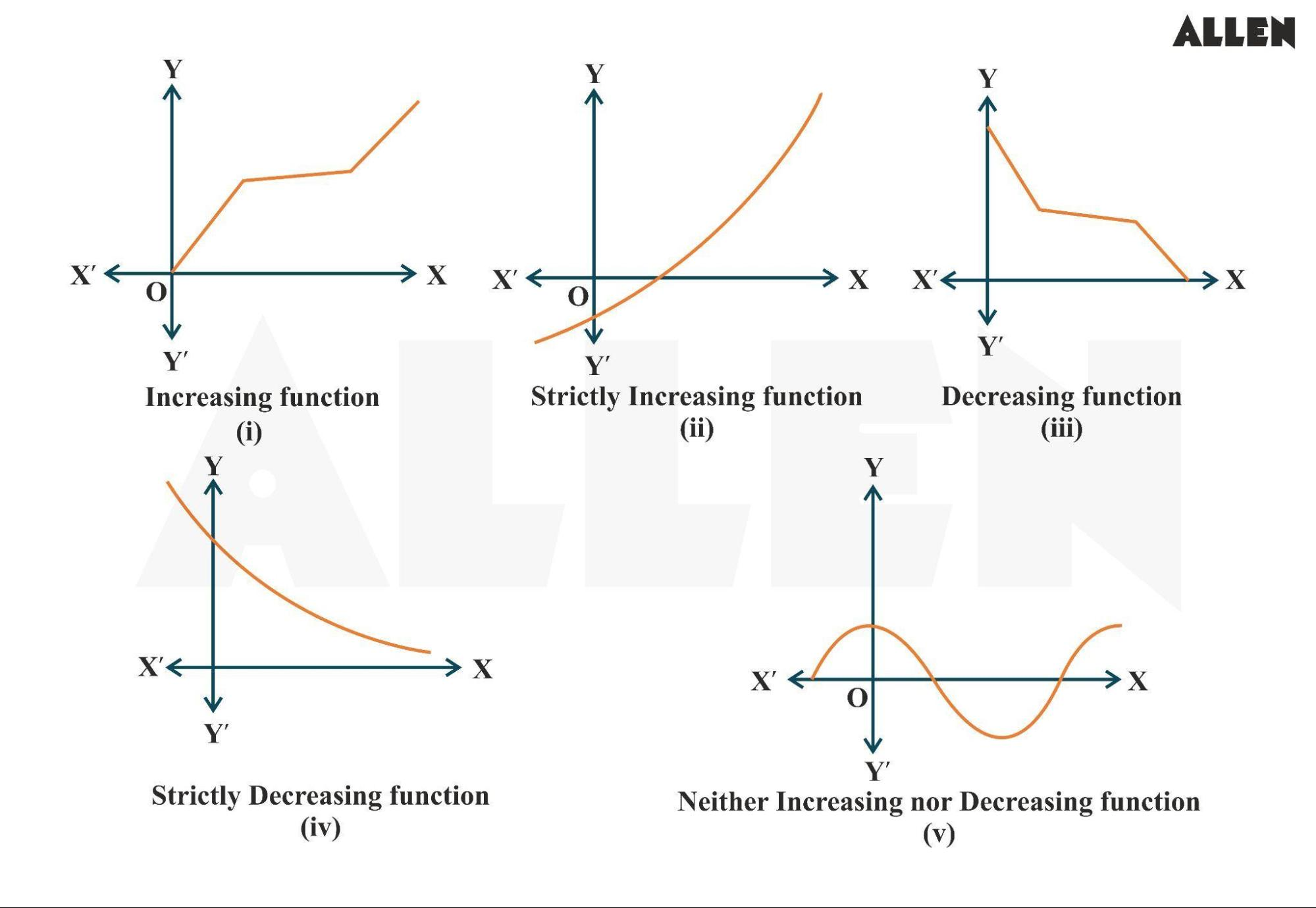
单调性概念
在区间上:
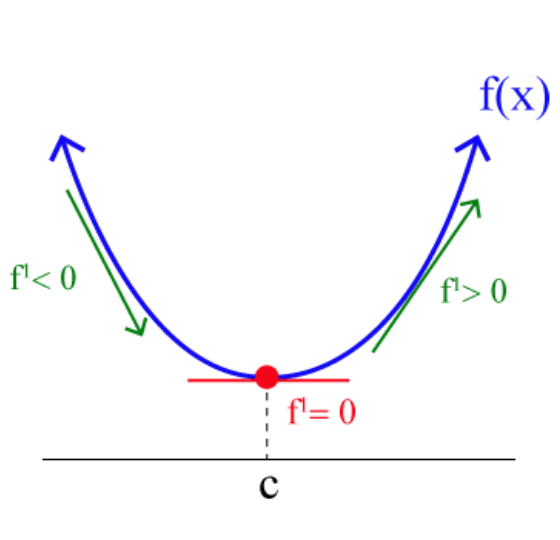
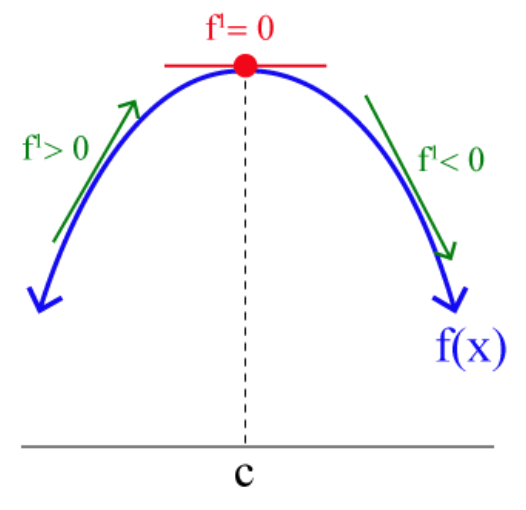
- 单调递增:若,有
- 单调递减:若,有
- 严格单调:将不等号改为严格不等号
判断方法
-
定义法
- 直接比较函数值
- 适用于简单函数
-
导数法
- :递增
- :递减
- :可能为极值点
单调区间
求解步骤
- 求导数
- 解得驻点
- 确定符号
- 划分单调区间
应用技巧
重要应用
-
方程求解
- 利用单调性确定解的存在性
- 确定解的个数
-
不等式证明
- 利用单调性比较函数值
- 转化为导数问题
常见错误
注意事项
- 导数为零不一定是极值点
- 单调性与连续性无必然联系
- 严格单调与非严格单调的区别
练习方向
练习建议
- 绘制函数图像分析单调性
- 用导数判断单调区间
- 结合实际问题应用单调性
- 证明函数的单调性
重要结论
核心定理
- 连续函数在闭区间上一定有最值
- 严格单调函数一定是一一对应的
- 单调函数的复合函数保持单调性
单调递增
单调递减