正弦定理

正弦定理与三角形外接圆之间有一个非常优雅的关系。$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R=d$。

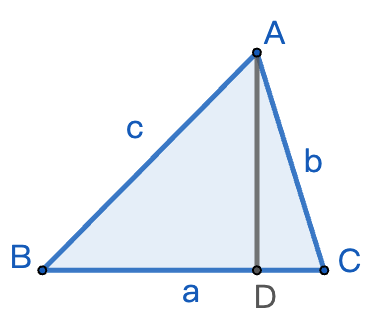
正弦定理的图形表示

翻转

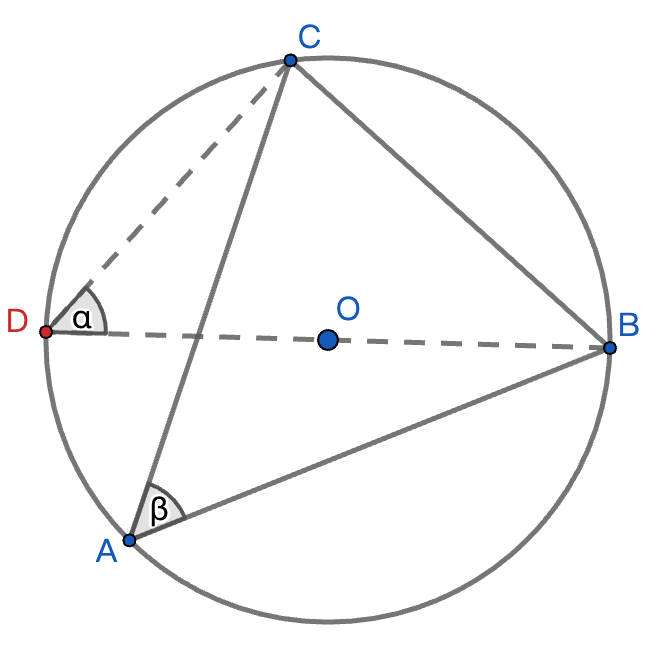
这个结果表明：

1. 正弦定理中的比值实际上等于三角形外接圆直径的长度。
2. 我们可以用外接圆半径 R 来表示正弦定理： $a=2R\sin A$ $b=2R\sin B$ $c=2R\sin C$
3. 这个关系提供了一种计算三角形外接圆半径的方法： $R=\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C}$
4. 它还揭示了三角形的边长、角度和外接圆半径之间的深刻联系。

这个定理是如何想出的？想想看。

graph TD
    A[任意三角形 ABC] --> B[外接圆]
    A --> C[直角三角形]
    B --> D[圆心角与内角关系]
    C --> E[边与正弦函数关系]
    D --> F[正弦定理]
    E --> F

    G[几何性质] --> B
    H[三角函数定义] --> E
    I[角度关系] --> D

    J[a/sinA = 2R] --> F
    K[b/sinB = 2R] --> F
    L[c/sinC = 2R] --> F

    F --> M[a/sinA = b/sinB = c/sinC]

    style G fill:#f9f,stroke:#333,stroke-width:2px
    style H fill:#ff9,stroke:#333,stroke-width:2px
    style I fill:#9ff,stroke:#333,stroke-width:2px
    style F fill:#f99,stroke:#333,stroke-width:2px