角的度量

角的度量有两种主要方法：角度和弧度。角度以度（°）为单位，一个完整的圆是360°；而弧度以圆的半径长度为基准，用弧长与半径的比值来表示角的大小。这两种度量方式可以相互转换，其中π（pi）是关键：180°恰好等于π弧度。

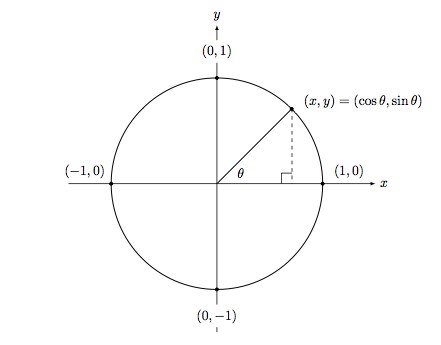
单位圆（半径为1的圆）在这里扮演着重要角色，它帮助我们直观理解弧度，并成为定义三角函数的基础。三角函数（如正弦、余弦）就是在单位圆上，不同角度或弧度对应的特定线段长度，这些函数为我们研究圆及周期性变化提供了强大的数学工具。

角度

• 定义：一个圆周被分为360等份，每份为1度（1°）
• 一周角 = 360°

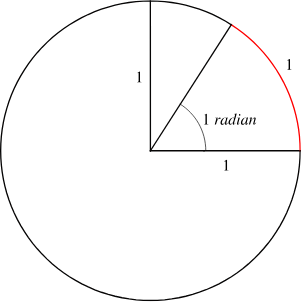
弧度

• 定义：弧长等于半径长的圆心角为1弧度（1 rad）
• 一周角 = 2π rad

转换关系

• π rad = 180°
• 1° = π/180 rad
• 1 rad ≈ 57.3°

转换公式

角度转弧度：$\text{角度}\times \frac{\pi \text{ radians}}{180^{\circ }}$ 弧度转角度：$\text{弧度}\times \frac{180^{\circ }}{\pi \text{ radians}}$

弧长公式

对于半径r的圆，角度$\theta$对应的弧长：$\text{弧长}=r\theta$ 若半径r=1，则弧长简化为$\theta$。

角度的认识

三角函数的本质是角度的测量，角度的本质是旋转和长度比值。度数、弧度都是角度的量化表示。三角函数、单位圆等都可成为对角度的研究方法。

预习问题

1. 角和角度概念上有何不同？

角是***，角度是***。

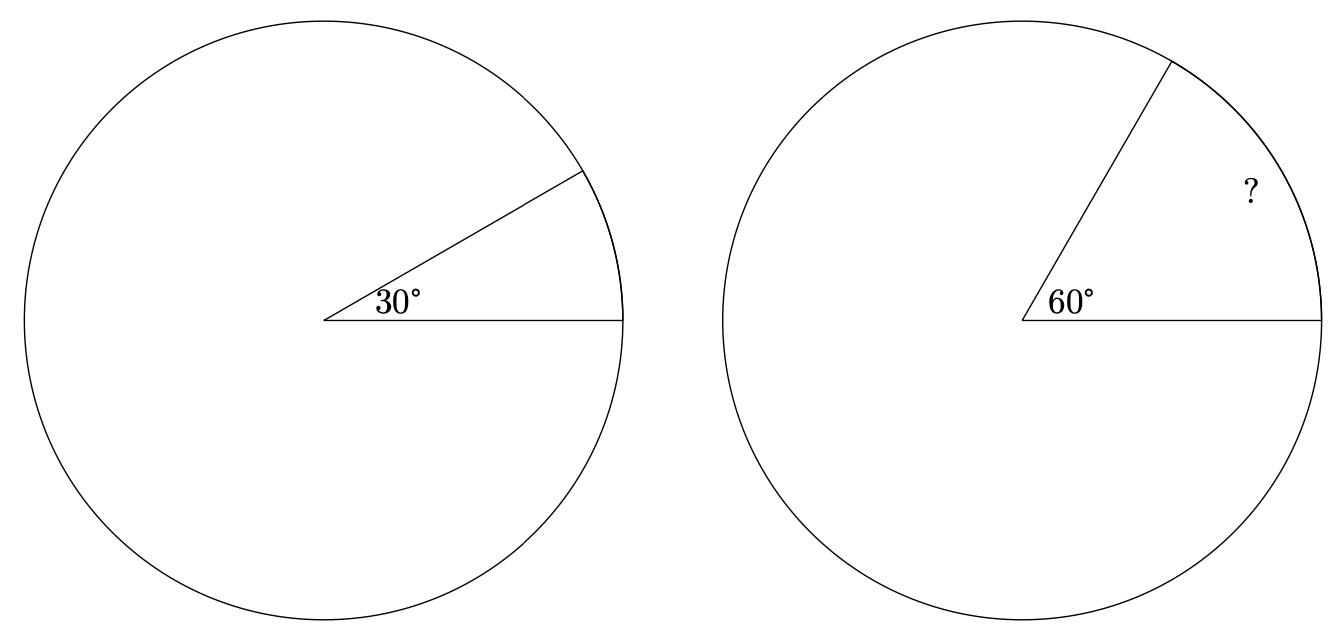
2. 如何在头脑中快速估算常见角度（如30°、45°、60°）对应的弧度值？

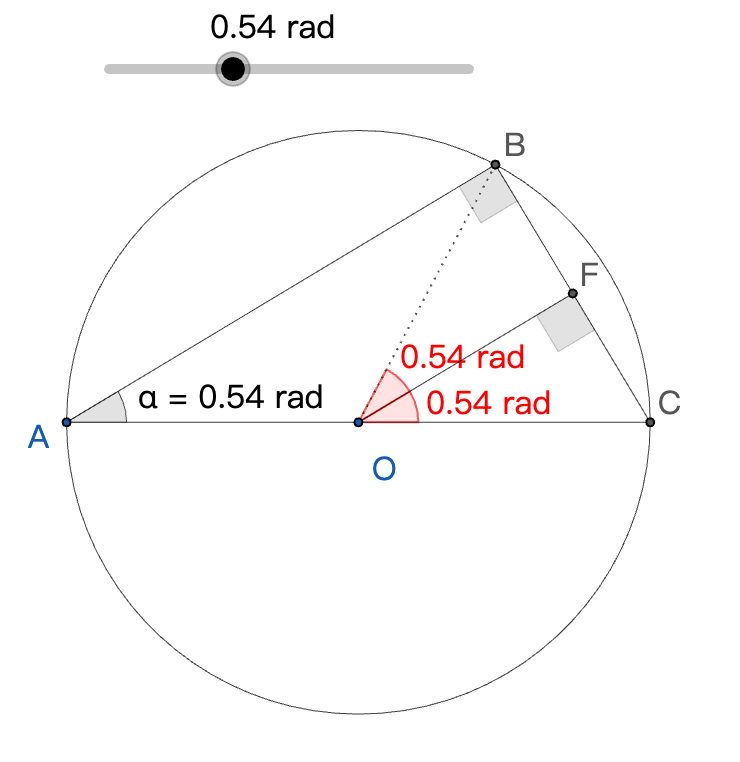
3. 在单位圆上，弧度和弧长之间有什么关系？

4. 已知三角形的三条边长，三角形的形状可唯一确定，但三个角度如何计算？

5. 还有什么其他方式可以表示角的大小？