贝叶斯思维教会我们如何根据新的信息来更新自己的认知和判断,这是成长和学习的核心,用一个游戏的例子学习贝叶斯概率:
问题:连续掷两次骰子,已知两次点数之和大于7的条件下,第一次掷出点数大于4的概率。
- A: 第一次掷出的点数大于4
- B: 两次掷出的点数之和大于7
我们要计算P(A|B),即在已知两次点数之和大于7的条件下,第一次掷出点数大于4的概率。
步骤分析:
- 计算先验概率P(A):
P(A) = 2/6 = 1/3 (5和6两个点数大于4)
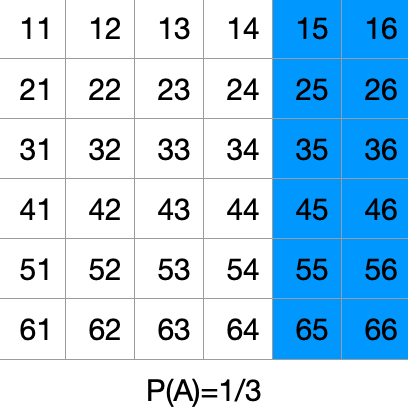
- 计算P(B):
P(B) = 15/36 (36种可能组合中,15种和大于7)

- 计算P(B|A):
当A发生时(第一次>4),第二次只需>2即可满足B
P(B|A) = 9/12=3/4
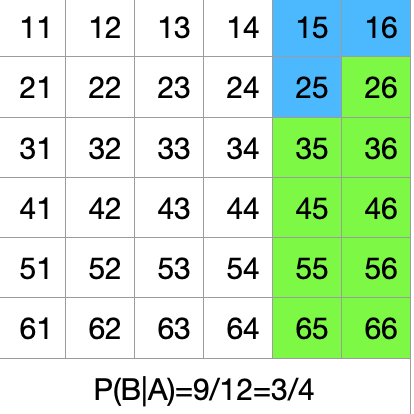
- 应用贝叶斯公式:
P(A|B) = P(B|A) * P(A) / P(B)
= (3/4) * (1/3) / (15/36)
= 9/15
= 0.60
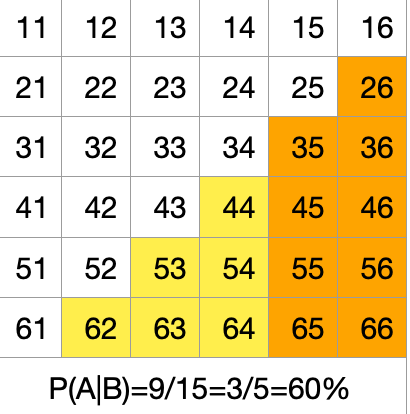
解释:
- 这个结果意味着,当我们知道两次点数之和大于7时,第一次掷出大于4点的概率为60%。
- 这比原本的先验概率(33.33%)高,因为我们有了新的信息(总和>7)。
概念图示:
graph TD
A[两次掷骰子]
B["先验概率 P(A)"]
C["条件概率 P(B|A)"]
D["边缘概率 P(B)"]
E[贝叶斯公式]
F["后验概率 P(A|B)"]
A --> B
A --> C
A --> D
B --> |1/3| E
C --> |3/4|E
D --> |15/36| E
E --> |3/5| F
关键理解:
- 先验知识: 我们开始时只知道掷骰子的基本概率。
- 新信息: 我们得知总和大于7。
- 更新信念: 基于新信息,我们更新了对第一次掷骰结果的看法。